
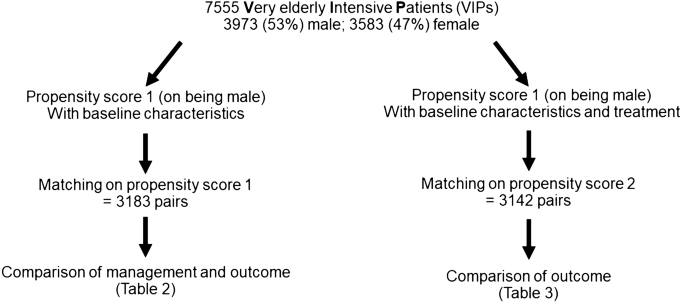
Standardized difference=(100*(mean(x exposed)-(mean(x unexposed)))/(sqrt((SD^2exposed+ SD^2unexposed)/2)) Second, we can assess the standardized difference. First, we can create a histogram of the PS for exposed and unexposed groups. We can use a couple of tools to assess our balance of covariates. if we have no overlap of propensity scores), then all inferences would be made off-support of the data (and thus, conclusions would be model dependent). If there is no overlap in covariates (i.e. This is true in all models, but in PSA, it becomes visually very apparent. Substantial overlap in covariates between the exposed and unexposed groups must exist for us to make causal inferences from our data. Matching without replacement has better precision because more subjects are used. Matching with replacement allows for reduced bias because of better matching between subjects. There is a trade-off in bias and precision between matching with replacement and without (1:1).
Matching with replacement allows for the unexposed subject that has been matched with an exposed subject to be returned to the pool of unexposed subjects available for matching. 1:1 matching may be done, but oftentimes matching with replacement is done instead to allow for better matches. The ratio of exposed to unexposed subjects is variable. If we go past 0.05, we may be less confident that our exposed and unexposed are truly exchangeable (inexact matching). Below 0.01, we can get a lot of variability within the estimate because we have difficulty finding matches and this leads us to discard those subjects (incomplete matching). This value typically ranges from +/-0.01 to +/-0.05. We set an apriori value for the calipers. We may not be able to find an exact match, so we say that we will accept a PS score within certain caliper bounds. The nearest neighbor would be the unexposed subject that has a PS nearest to the PS for our exposed subject. Most common is the nearest neighbor within calipers. Discarding a subject can introduce bias into our analysis. If we cannot find a suitable match, then that subject is discarded. We want to match the exposed and unexposed subjects on their probability of being exposed (their PS). We calculate a PS for all subjects, exposed and unexposed. The more true covariates we use, the better our prediction of the probability of being exposed. We use the covariates to predict the probability of being exposed (which is the PS). If we are in doubt of the covariate, we include it in our set of covariates (unless we think that it is an effect of the exposure). We may include confounders and interaction variables. We do not consider the outcome in deciding upon our covariates. We want to include all predictors of the exposure and none of the effects of the exposure. We use these covariates to predict our probability of exposure. Calculate the effect estimate and standard errors with this match population. Check the balance of covariates in the exposed and unexposed groups after matching on PS.ĥ. Match exposed and unexposed subjects on the PS.Ĥ. Use logistic regression to obtain a PS for each subject.ģ.
Decide on the set of covariates you want to include.Ģ. PSA helps us to mimic an experimental study using data from an observational study. But we still would like the exchangeability of groups achieved by randomization. There are several occasions where an experimental study is not feasible or ethical. One of the biggest challenges with observational studies is that the probability of being in the exposed or unexposed group is not random. Therefore, we say that we have exchangeability between groups. This equal probability of exposure makes us feel more comfortable asserting that the exposed and unexposed groups are alike on all factors except their exposure. Therefore, a subject’s actual exposure status is random. The probability of being exposed or unexposed is the same. Thus, the probability of being unexposed is also 0.5. randomized control trials), the probability of being exposed is 0.5. Exchangeability is critical to our causal inference. Propensity score analysis (PSA) arose as a way to achieve exchangeability between exposed and unexposed groups in observational studies without relying on traditional model building. Thus, the probability of being exposed is the same as the probability of being unexposed. We can match exposed subjects with unexposed subjects with the same (or very similar) PS. Once we have a PS for each subject, we then return to the real world of exposed and unexposed. We can calculate a PS for each subject in an observational study regardless of her actual exposure. In fact, it is a conditional probability of being exposed given a set of covariates, Pr(E+|covariates).


 0 kommentar(er)
0 kommentar(er)
